A tree-based machine learning method splits the space into regions and fits a region-specific classification/regression function (typically just a constant). Additional flexibility and capacity can be achieved by bagging and boosting elementary trees, but at the core of these methods is their space partitioning capabilities. A few months ago I started to wonder if neural networks can do a similar thing. My gut feeling was that neural nets should be doing something of the kind, but the mechanics of the neural net space partitioning was unclear to me. I even posted a question on StackExchange, yet, I have not gotten an answer.

However, I recently discovered an insightful video lecture by Ian Goodfellow where he elaborates on the nature of adversarial examples and discusses possible ways to defend from an attacker (spoiler alert: there seems to be no working method yet!). Basically, he argues that adversarial examples is a common Achilles' heel, which comes—in fact somewhat surprisingly—from excessive linearity of existing approaches. Ian Goodfellow argues that this issue plagues almost all standard machine learning approaches including SVMs, tree-based methods, and neural networks. What is even more surprising, adversarial examples are transferable across different algorithms: An adversarial example designed to fool, e.g., a decision tree is very likely to fool some other method as well!

Fig 1. A hyperplane separating positive and negative examples.

Ian also notes that neural nets divide the space using an approximately piecewise linear function. This observation basically answers my question about the space partitioning capabilities of neural networks. For neural nets with only truly piecewise linear activation functions (such as RELU), the division of the space is truly linear. As a side comment, this kinda explains (at least for me) the ability of neural networks to generalize quite well despite having so many parameters. A well-known deficiency of the linear and piecewise linear models (as noted by Ian) is that they can be super confident in regions where they encountered no training data. For example, in Figure 1 the linear classifier would have a very strong "opinion" about the negativity of the point marked by the red question mark. However, this confidence is not fully substantiated, because there are no training points nearby.

Adversarial examples notwithstanding, I think it may be useful to get a better understanding of the space partitioning "mechanics" of the neural networks. In my case, such understanding came from reading a very recent paper AN UPPER-BOUND ON THE REQUIRED SIZE OF A NEURAL NETWORK CLASSIFIER by Hossein Valavi and Peter J. Ramadge. The paper is unfortunately paywalled, but the slides are publicly available.

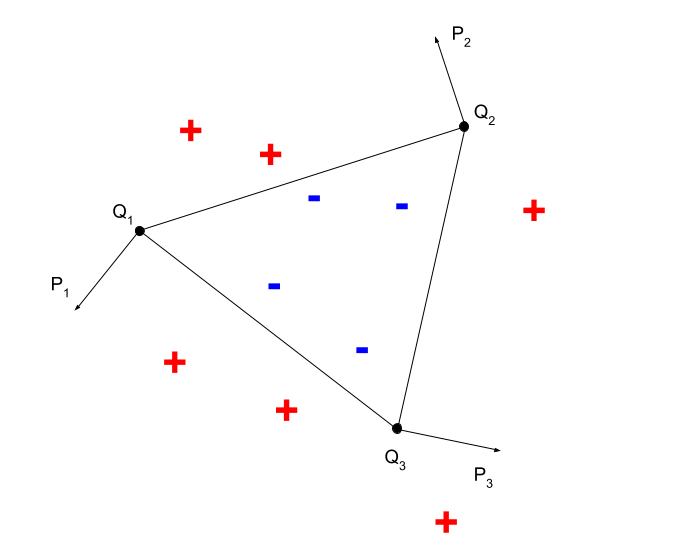
Fig 2. A convex shape (triangle) classifier.

In this paper, authors remind us that neural nets possess two powerful capabilities: an ability to distinguish data points separated by a given hyperplane and a capacity to implement arbitrary logic circuits (they also prove facts about complexity of such circuits, but these proofs are not very relevant to our discussion). Without going into technicalities right away (but some are nevertheless discussed below), this means that neural nets can easily divide a real-vector space using polytopes, e.g., convex ones. Let us consider a simple example of a piecewise linear classifier in Fig. 2. As we can see positive and negative training examples can be separated from each other using three planar hyperplanes, simply speaking by three lines. Positive and negative examples are located on the opposite sides of these separating lines. Therefore, a condition of belonging to a negative class can be written as : $\langle x - Q_1, P_1 - Q_1 \rangle < 0 \mbox{ and } \langle x - Q_2, P_2 - Q_2 \rangle < 0 \mbox{ and } \langle x - Q_3, P_3 - Q_3 \rangle < 0$. This condition can be easily implemented with a two layer neural networks with the sign activation function.

Because neural nets can have tons of parameters, they can slice and dice the space at least as well as tree-based learning algorithms. In fact, if necessary, given enough parameters, we can always achieve a perfect separation of data points from different classes (assuming consistent labeling). For example, we can place each positive-class datapoint into its own hyperhube and implement neural nets that "fire" only for training data points in these hypercubes. We will then combine these nets using an OR circuit. Of course, such construct is extremely inefficient and does not generalize well, but it IMHO illustrates the basic space-partitioning powers of the neural nets.

In conclusion, I discuss some technical details, which are primarily of the theoretical interest. For simplicity of exposition I consider only the binary classification scenario. First, let us consider again a hyperplane that divides the space into two subspaces. The claim is that we can always construct a neural network that maps points on one side of the hyperplane to zeros (negative) and points on the other side of the hyperplane to ones (positive). This fact is trivial for neural networks with the sign activation function (a sign of the scalar product between data points and the hyperplane-orthogonal vector defines the class of a data point). We illustrate this point in Figure 1. However, it is more work to prove for differentiable activation functions such as RELU (which are actually used in practice nowadays). This is done in Lemma 3.1 of the mentioned paper.

Once we divide the space into regions and implement all neural networks that fire exactly when a data point is in its region, we need to combine these classifiers using a boolean circuit. Consider again an example in Fig. 2 In this case a boolean circuit is a simple three-variable conjunction.

There are certainly many ways to implement a binary logic circuit using a neural network. One of these is briefly outlined Corollary 3.3. This Corollary is a bit hard to parse, but, apparently, authors propose to solve a problem in two steps. First, they suggest to map each combination of $n$ zeros and ones to a single-coordinate data point in a $2^n$-dimensional space. Because circuit values can be true or false, there will be "true" or "false" data points in the target $2^n$-dimensional space. If coordinate values of true and false points are different, these points are linearly separable (e.g., a "true" data point has exactly one dimension with value one and a "false" data point has exactly one dimension with value two). Thus, according to their Lemma 3.1, there would exist a second neural network based function that maps true points to one and false points to zeros.

Authors do not describe how to implement the mapping to the $2^n$ dimensional space, but we can use the following combination of RELU-activated threshold circuits:

Given a binary input variables $x_i$ this function is equal to one if and only if the input is the same as the binary representation of $k$.

UPDATE: quite interestingly a recent paper provides a more specific characterization of functions represented by feed-forward neural networks with RELU activations. Namely, this is a subclass of rational functions belonging to the family of tropical rational maps (a tropical map is piecewise linear).