 |
|
|
|
 |
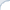 |
 |
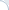 |
 |
 |
 |
Submitted by srchvrs on Thu, 03/28/2024 - 22:41
Attention folks working on LONG-document ranking & retrieval! We found evidence of a very serious issue in existing long-document collections, most importantly MS MARCO Documents. It can potentially affect all papers comparing different architectures for long document ranking.
Do not get us wrong: We love MS MARCO: It has been a fantastic resource that spearheaded research on ranking and retrieval models. In our work we use MS MARCO both directly as well as its derivative form: MS MARCO FarRelevant.
Yet MS MARCO (and similar collections) can have substantial positional biases which not only "mask" differences among existing models, but also prevent MS MARCO trained models from performing well on some other collections.
This is not a modest degradation where performance drops roughly to BM25 level (as we observed, e.g., in our prior evaluation).. It can be a dramatic drop in accuracy down to the random baseline level.
We found a substantial positional bias of relevant information in standard IR collections, which include MS MARCO Documents and Robust04. However, judging from other paper results a lot of other collections are affected.
Because relevant info tends to be in the beginning of a doc we often do not need a special long-context model to do well in ranking and retrieval. The so-called FirstP model (truncation to < 512 tokens) can do well (see the picture, we do not plot FirstP explicitly, but all the numbers are relative to FirstP efficiency or accuracy):
So how do we prove positional bias is real? There is no definitive evidence, but we provide several evidence pieces. In doing so we introduce a NEW synthetic collection MS MARCO Far Relevant which does not have relevant passages in the beginning.
- On MS MARCO we trained 20+ rank models (including two FlashAttention-based models) and observed all of them to barely beat FirstP (in rare cases models underperformed FirstP);.
- We analyzed positions of relevant passages and found these to be skewed to the beginning;
- We 0-shot tested & then fine-tuned models on MS MARCO Far Relevant.
Unlike standard collections where we observed both little benefit from incorporating longer contexts & limited variability in model performance (within a few %), experiments on MS MARCO FarRelevant uncovered dramatic differences among models.
-
To begin with, FirstP models performed roughly at the random-baseline level in both 0-shot and fine-tuning scenarios (see the picture below).
-
Second, simple aggregation models including MaxP and PARADE Attention had good zero-shot accuracy, but benefited little from fine-tuning.
-
In contrast, most other models had poor 0-shot performance (roughly at a random baseline level), but outstripped MaxP by as much as 13-28% after fine-tuning. Check out the lines connecting markers in left and right columns:
Best models? PARADE models were the best and markedly outperformed FlashAttention-based models, Longformer as well as chunk-and-aggregate approaches. PARADE Attention performed best on standard collection (in most cases) and in the zero-shot transfer model on MS MARCO FarRelevant. However, among fine-tuned models on MS MARCO Far Relevant, the best was PARADE Transformer (with a randomly initialized aggregator model).
This paper is an upgrade of 2021 preprint enabled by a great collaborator David Akinpelu as well as by the team of former CMU (MCDS) students. David, specifically, did a ton of work including implementation of recent baselines.
Paper link.
Code/Data link
Submitted by srchvrs on Tue, 08/26/2025 - 19:08
I recently finished, perhaps, my nerdiest computer science paper so far and it was accepted by TMLR: A Curious Case of Remarkable Resilience to Gradient Attacks via Fully Convolutional and Differentiable Front End with a Skip Connection. This work was done while I was at the Bosch Center of AI (outside my main employment at Amazon), but I was so busy that I had little time to put it in writing. I submitted the first draft only last year, and it required a major revision, which I was able to finish only in July. It is not a particularly practical paper—I accidentally discovered an interesting and puzzling phenomenon and decided to document it (with a help of my co-authors).
The following AI-generated summary, I believe, provides an accurate description of our work:
The paper presents a fascinating case study on how a seemingly innocuous modification to a neural network can drastically alter its perceived robustness against adversarial attacks. I accidentally discovered a simple yet surprisingly effective technique: prepending a frozen backbone classifier with a differentiable and fully convolutional "front end" model containing a skip connection. This composite model, when trained briefly with a small learning rate, exhibits remarkable resistance to gradient-based adversarial attacks, including those within the popular AutoAttack framework (APGD, FAB-T).
Here's a breakdown of the paper's core elements, methodology, and findings in more detail:
1. The Curious Phenomenon:
-
We observed that adding a differentiable front end to a classifier significantly boosted its apparent robustness to adversarial attacks, particularly gradient-based ones.
-
This robustness occurred without significantly sacrificing clean accuracy (accuracy on non-adversarial, original data).
-
The effect was reproducible across different datasets (CIFAR10, CIFAR100, ImageNet) and various backbone models (ResNet, Wide ResNet, Vision Transformers).
-
The training recipe for the front end (small learning rate, short training duration) was stable and reliable.
2. The Front End Architecture (DnCNN):
-
The front end used is based on DnCNN (Denoising Convolutional Neural Network), a fully convolutional architecture with skip connections.
-
Skip connections are crucial for training deep networks. They help the gradient flow more smoothly during backpropagation, preventing vanishing gradients.
-
DnCNN is differentiable. Unlike some adversarial defense strategies that rely on non-differentiable components (like JPEG compression) to disrupt gradient-based attacks, DnCNN allows gradients to be computed throughout the entire network.
-
We argue that the success of this method is especially surprising because the use of a skip connection is actually expected to improve gradient flow, not to mask gradients.
Submitted by srchvrs on Thu, 08/18/2022 - 00:37
The Hugging Face Accelerate library provides a convenient set of primitives for distributed training on multiple devices including GPUs, TPUs, and hybrid CPU-GPU systems (via Deepspeed). Despite convenience, there is one drawback: Only a synchronous SGD is supported. After gradients are computed (possibly in a series of accumulation steps), they are synchronized among devices and the model is updated. However, gradient synchronization is costly and it is particularly costly for consumer-grade GPUs, which are connected via PCI Express.
For example, if you have a 4-GPU server with a 16-lane PCI express v3, your synchronization capacity seems to be limited to 16 GB per second [1]. Without fast GPU interconnect, gradient synchronization requires transferring of each model weights to CPU memory with subsequent transfers to three other GPUs. This would be 16 transfers in total. If PCI express is fully bidirectional (which seems to be the case), this can be done a bit more efficiently (with 12 transfers) [2]. According to my back-of-the-envelope estimation gradient synchronization can take about the same time as training itself [3]! Thus, there will be little (if any) benefit of multi-GPU training.
Without further speculation, let us carry out an actual experiment (a simple end-to-end script to do so is available). I train a BERT large model for a QA task using two subsets of SQuAD v1 dataset (4K and 40K samples) using either one or four GPUs. Each experiment was repeated three times using different seeds. All results (timings and accuracy values) are provided.
In the multi-GPU setting, I use either a standard fully synchronous SGD or an SGD that synchronizes gradients every K batches. Note that the non-synchronous variant is hacky proof-of-concept (see the diff below), which likely does not synchronize all gradients (and it may be better to synchronize just model weights instead), but it still works pretty well.
For the fully synchronous SGD, each experiment is carried out using a varying number of gradient accumulation steps. If I understand the code of Accelerate correctly, the more accumulation steps we make, the less frequent is synchronization of gradients, so having more accumulation steps should permit more efficient training (but the effective batch size increases).
# of training
samples |
Single-GPU |
Multi-GPU (four GPUs)
fully synchronous SGD
varying # of gradient accumulation steps |
Multi-GPU (four GPUs)
k-batch synchronous SGD
varying # of gradient synchronization steps |
|---|
|
|
1 |
2 |
4 |
8 |
16 |
1 |
2 |
4 |
8 |
16 |
| 4000 |
f1=79.3 |
f1=77.8 2.6x |
f1=74.7 2.7x |
f1=70.6 2.7x |
f1=54.8 2.9x |
f1=15.9 3.1x |
f1=77.4 2.6x |
f1=74.5 2.9x |
f1=71.9 3.3x |
f1=72.8 3.5x |
f1=74.2 3.6x |
| 40000 |
f1=89.2 |
f1=88.6 2.4x |
f1=88.2 2.5x |
f1=87.5 2.6x |
f1=86.7 2.6x |
f1=84.4 2.6x |
f1=88.8 2.4x |
f1=87.2 2.8x |
f1=87.3 3.2x |
f1=87.4 3.4x |
f1=87.3 3.6x |
The result table shows both the accuracy (F1-score) and the speed up with respect to a single-GPU training. First, we can see that using a small training set results in lower F1-scores (which is, of course, totally expected). Second, there is a difference between single-GPU training and fully-synchronous SGD, which is likely due to increase in the effective batch size (when all four GPUs are used). For the larger 40K training set the degradation is quite small. In any case, we use F1-score for the fully synchronous multi-GPU training as a reference point for the perfect accuracy score.
When we use the fully synchronous SGD, the increase of the number of gradient accumulation steps leads only to a modest speed up, which does not exceed 2.6x for the larger 40K set. At the same time, there is a 5% decrease in F1-score on the larger set and a catastrophic 3x reduction for the 4K set! I verified this dramatic loss cannot be easily fixed by changing the learning rate (at least I did not find good ones).
In contrast, for the non-synchronous SGD, there is a much smaller loss in F1-score when the synchronization interval increases. For the larger 40K training set, synchronizing one out of 16 batches leads to only 1.7% loss in F1-score. In that, the speed-up can be as high as 3.6x. Thus, our POC implementation of the non-synchronous SGD, which as I mentioned earlier is likely to be slightly deficient, is (nearly) always (often much) better than the current fully synchronous SGD implemented in Accelerator.
To reiterate, Accelerator supports only the synchronous SGD, which requires a costly synchronization for every batch. This is not an efficient setup for servers without a fast interconnect. A common "folklore" approach (sorry, I do not have a precise citation) is to relax this requirement and synchronize model weights (or accumulated gradients) every K>1 batches [4]. This is the approach I implemented in FlexNeuART and BCAI ART. It would be great to see this approach implemented in Accelerator as well (or directly in Pytorch).
Notes:
[1] Interconnect information can be obtained via nvidia-smi -a.
[2] I think fewer than 12 bidirectional transfers would be impossible. Optimistically we can assume updated weights/gradients are already in the CPU memory, then each model weights/gradients need to be delivered to three other GPUs. In practice, 12 transfers are actually possible by moving data from one GPU's memory to CPU memory and immediately to another GPU's memory. After four such bi-directional transfers all data would be in the CPU memory. Thus, to finalize the synchronization process we would need only eight additional unidirectional (CPU-to-GPU) transfers.
[3] For a BERT large model (345M parameters) with half-precision gradients each gradient synchronization entails moving about 0.67 GB of data. As mentioned above, synchronization requires 12 bidirectional transfers for a total of 12 x 0.67 = 8GB of data. Thus, we can synchronize only twice per second. At the same time, when using a single GPU the training speed of BERT large on SQuAD QA data is three iteration/batches per second. Thus, gradient synchronization could take about the same time as training itself! My back-of-the-envelope calculations can be a bit off (due to some factors that I do not take into account), but they should be roughly in the ballpark.
[4] The parameter value K needs to be tuned. However, I find that its choice does not affect accuracy much unless K becomes too large. Thus it is safe to increase K until we achieve a speed-up close to the maximal possible one (e.g., 3.5x speed up with four GPUs). In my (admittedly limited) experience, this never led to noticeable loss in accuracy and sometimes it slightly improved results (apparently because non-synchronous SGD is a form of regularization).
A partial diff. between the original (fully-synchronous) and K-batch synchronous trainer (this is just a POC version, which is not fully correct):
@@ -760,6 +767,9 @@ num_training_steps=args.max_train_steps, ) + orig_model = model + orig_optimizer = optimizer + # Prepare everything with our `accelerator`. model, optimizer, train_dataloader, eval_dataloader, lr_scheduler = accelerator.prepare( model, optimizer, train_dataloader, eval_dataloader, lr_scheduler @@ -834,6 +845,7 @@ for epoch in range(starting_epoch, args.num_train_epochs): model.train() + orig_model.train() if args.with_tracking: total_loss = 0 for step, batch in enumerate(train_dataloader): @@ -842,17 +854,27 @@ if resume_step is not None and step < resume_step: completed_steps += 1 continue - outputs = model(**batch) + grad_sync = (step % args.no_sync_steps == 0) or (step == len(train_dataloader) - 1) + if grad_sync: + curr_model = model + curr_optimizer = optimizer + else: + curr_model = orig_model + curr_optimizer = orig_optimizer + outputs = curr_model(**batch) loss = outputs.loss # We keep track of the loss at each epoch if args.with_tracking: total_loss += loss.detach().float() loss = loss / args.gradient_accumulation_steps - accelerator.backward(loss) + if grad_sync: + accelerator.backward(loss) + else: + loss.backward() if step % args.gradient_accumulation_steps == 0 or step == len(train_dataloader) - 1: - optimizer.step() + curr_optimizer.step() lr_scheduler.step() - optimizer.zero_grad() + curr_optimizer.zero_grad() progress_bar.update(1) completed_steps += 1 @@ -896,6 +918,7 @@ all_end_logits = [] model.eval() + orig_model.eval() for step, batch in enumerate(eval_dataloader): with torch.no_grad():
Submitted by srchvrs on Thu, 09/02/2021 - 09:02
I read an interesting and thought-provoking study by Negar Arabzadeh and co-authors arguing that MS MARCO official relevant documents tend to be inferior to top-documents returned by modern (BERT-based) neural rankers. This may indicate there was a bias in the original data set creation procedure. Some people rushed to conclude that this study rendered the IR leaderboards to be completely inadequate as a tool to measure progress. I believe this is an overstatement. Below I provide more detailed explanations. The paper (and the original variant of this blog post) caused lengthy Facebook and e-mail discussions, which convinced me to revise the blog post. Two particular points/questions were: (1) The crowd-sourcing procedure itself may introduce a bias, (2) Given a modest (~500) number of re-annotated queries, how likely is it to observe a similar shift in rankings due to a random selection of queries?
The study in question uses crowd-sourcing to re-evaluate several high performing runs (on the MS MARCO passage-ranking leaderboard) using a subset of about 500 MS MARCO queries. Authors asked crowd workers to directly compare all pairs of top documents returned by these top systems, which allowed them to create a new set of relevance judgements. In this crowd-sourcing experiment authors learned that when a neural ranker and MS MARCO relevance data disagreed on a top passage, the top result from the neural ranker was actually better in about 66% of the cases. They also found that when there was an agreement on the top passage between the MS MARCO data and the neural ranker, crowd-workers preferred that top passage to the second one in also about 66% of the cases, which is an important sanity check indicating a high/reasonable quality of the crowd-sourced data.
Missing important relevant answers is not necessarily a concern if the answers are missing completely at random, without creation of a pattern where system A consistently ranks missing relevant items higher than system B. In that, there is a disagreement on whether the study convincingly proves that such a pattern exists.
First, the study uses a tournament system to select best/preferred answers, which are uniformly better than other answers. This is not compatible with the original MS MARCO annotation strategy where there was no goal to identify the best answers. It may be the case that the new annotation procedure is itself biased. It will be, nevertheless, interesting to carefully examine the preferred relevant answers found by the tournament procedure to assess how they are different from documents that have a positive MS MARCO (relevance) label.
Second, the study uses a relatively small subset of MS MARCO queries (about 10% of the complete set), which can easily introduce substantial randomness. We previously found that small query sets were not reliable. In contrast, creators of MS MARCO showed there was a surprising stability of the ranking under bootstrapping (see Table 1 and 2) when one uses a fully set of queries (to sample from).
Let us now review some results that authors obtained with the crowd-sourced relevance judgements. Despite a shake-up of the ranking due to use of crowd-sourced judgements (instead of original MS MARCO labels) and a low correlation in before-after ranks, there is a clear trend (Figure 5) to rank recent top-performing leaderboard systems higher than older low-performing ones. One notable outlier is run L (RepBERT), which could have been much more effective than the leaderboard suggests. However, in the crowd-sourcing based re-evaluation L is still ranked lower than the top leaderboard run A. Furthermore, L has 0.1 lower MRR compared to runs B, C (and others) that perform best (or nearly so) in this crowd-sourcing experiment. These runs perform much better on the official leaderboard as well.
To conclude, I note that authors propose to set up a continuous evaluation procedure where a set of relevance judgements is reassessed as new runs are added. We all agree that it will be an interesting experiment to run. However, it may be difficult to pull off.
Submitted by srchvrs on Thu, 07/01/2021 - 11:48
UPDATE: Not all of what I wrote aged well so certain corrections are required. It was a right observation (described below) that in a zero-shot mode when a model creates code directly from an arbitrary prompt (i.e., it is not shown several text-to-code translation examples), GPT-3 (or similar models) that were not systematically trained on code performed rather poorly. However, a subsequent work by Open AI: Evaluating Large Language Models trained on Code" showed that if a model was pre-trained on lot of publicly available code then it acquired non-trivial coding capabilities often producing correct (or near correct) solutions purely from natural language. A more up-to-date perspective is in my more recent tweet.
Automation of software development is as old as the software development itself. Remember that we started writing programs directly in machine codes (and I personally actually have experience programming such a device). Then, a big productivity boost was achieved by writing assembly programs, which shortly followed by introduction of higher-level languages such as FORTRAN. The progress clearly has not stopped at that point and we see a great deal of improvement coming from better programming languages, libraries, and tooling. In the machine learning world, people started by writing their own CUDA kernels, but now we have dynamic tensor frameworks (such as Pytorch), where the neural computation graph is defined (and modified) by a Python program. These modifications can happen dynamically, i.e., during training or inference. There are a lot of smart ways in which the progress can continue in the future. But I think that a fully automated code generation from a natural language is not one of them.
What are the problems with automatic code generation? One big issue is that there is no reliable technology to understand and interpret the natural language. My strong belief is that sequence-to-sequence like neural networks or language-modeling approaches do not learn much beyond a probability distribution. These technologies are ground-breaking and there is nothing short of amazing that we can have a close-to-human-quality machine translation. However, these models do make stupid mistakes here and there. Humans do them too, but the output of a machine translation system is easy to post-edit and the scale of errors can be pretty small. What makes it possible is that the machine translation is (loosely speaking) a content-preserving process, which has a high degree of fidelity in terms of lexical, syntactic and semantic similarity between the source and the target. It also has a high degree of locality: A sentence-level translation, which does not take the document context into account, can sometimes be quite accurate. This is one of the reasons why the machine translation was possibly the first successful AI application, which was shown to work in a very narrow domain more than 50 years ago.
Many people think that post-editing of the GPT3 output would work as well as post editing of the machine translation output. However, software development is far from this idealistic view. Software is being created as a fusion of a developer's knowledge and common sense, user requirements, colleague advice and feedback. There is no well-defined source and no well-defined target. There is also a complicated feedback loop coming from debugging and testing. It is simply impossible to express these requirements through a reasonably small set of examples. Furthermore, writing out such examples is time consuming and error prone (there is no precise semantics in example-based programming). It is even more time consuming to fix the mistakes generators make.
I also strongly believe that the current AI systems can greatly help to improve the autocomplete functionality, but pushing the current tech to the level of a "pilot"-like automation is likely impossible. Unfortunately, much of the discussion on the topic is influenced by early testers whose positive feedback has been magnified 1000x while all the negative feedback has been largely muffled. Fortunately, the
EleutherAI and HuggingFace teams made a GPT-neo demo available to everyone and we can now poke it. We are interested in the SQL generation, which is the only code-generation option.
First, one can notice that the process is not deterministic: Each time you click "generate" the system may generate a unique answer. The original HuggingFace example asks to "Fetch the three max salaries from the Worker table". I clicked multiple times, but all of the answers seem to be incorrect. Sometimes, they are quite far from a correct one, check out, e.g., this example:

I also tried to replace the word "fetch" with the word "select" in the prompt, but the results were still disastrous. One may argue that EleutherAI/HuggingFace came up with the prompt that was too complicated. Thus, I tried a simpler version, which had more consistent prompts:
Q: Select worker IDs whose salaries are greater than one thousand.
A: SELECT WORKER_ID WHERE SALARY > 1000;
###
Q: Select worker IDs whose salaries are greater than 2345.
A: SELECT WORKER_ID WHERE SALARY > 2345;
###
Q: Fetch worker IDs whose salaries are greater than three thousands.
A: SELECT WORKER_ID WHERE SALARY > 3000;
###
Q: Fetch worker IDs whose salaries are between 1500 and 2500.
A: SELECT WORKER_ID WHERE SALARY BETWEEN 1500 AND 2500;
###
Q: Fetch worker IDs whose salaries are greater than 4321.
A:
This prompt consistently generates a correct answer. However, the system still breaks easily, e.g., when I ask to retrieve salaries greater than four thousand and two hundred:

In conclusion, there is little doubt that language-to-code generation works in some toy cases, but in most other cases, it does not. I suspect that the technology is not there yet: It is completely unclear how the current predictive tech, which Metzler et al called dilettante, can be taken close to the level of accuracy of modern compilers, which is necessary, in fact, to be useful. Of course, the GPT-3 trained by Microsoft and OpenAI is better than the EleutherAI/HuggingFace GPT3, in particular, because it was trained in a semi-supervised fashion. Yet, its generation algorithm comes without any accuracy guarantees, which makes the model dangerous. In any case, I am looking forward to testing it, but Microsoft/OpenAI coding "co-pilot" is not open to the general public yet (there is a wait list).
Pages

|
|
 |
 |
 |
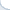 |
 |
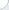 |
 |
|
|